Translate
This phase is the direct manipulation of the S-expression construct we left off of in the frontend phase.
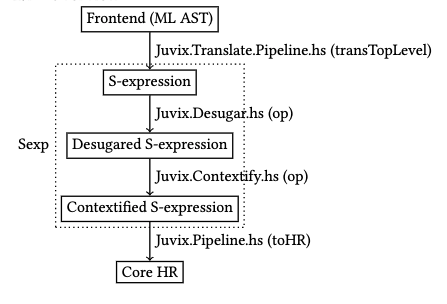
This section is broken up into three section, each growing in complexity as we go along. These are:
Desugaring
Every important operation in this phase is a direct Syntax to
Syntax transformation with no extra context needed.

The function op pipes all desugaring functions that do not require a context.
-- | @op@ fully desugars the frontend syntax from the original
-- frontend s-exp representation to a form without modules, conditions,
-- guards, etc. This pass thus does all transformations that do not
-- requires a context
op :: [Sexp.T] -> [Sexp.T]
op syn =
syn
>>| Pass.moduleTransform
>>| Pass.moduleLetTransform
>>| Pass.condTransform
>>| Pass.ifTransform
>>| Pass.multipleTransLet
|> Pass.multipleTransDefun
|> Pass.combineSig
>>| Pass.removePunnedRecords
>>| Pass.translateDoThe order of these passes is relatively arbitrary. We simply
remove modules, then module lets, then conds, then …, and then
do. The op function is ran directly on the output of the last phase.
Examples of its use are provided in the EasyPipeline module (run desugar1 and desugar2
to test the results for yourself!).
Desugaring S-expressions, Structurally
Structurally here refers to a systematic way of manipulating s-expressions in which form has and equivalent Haskell ADT.
Before getting into all the functions in op, such as Pass.moduleTransform, we first discuss the underlying tool that allows us to handle these passes in a principled way.
We'll use the let/defun form as an example of this transformation.
This code can be found in the Structure module.
;; From Design/S-expression Syntax
(:defun foo (x)
(:cond
((:infix == x 2) (:infix + 3 (:infix + 4 x)))
(else (:infix + x 2))))defun is broken into the name foo, the arguments x
(note this can pattern match), and the body cond.
In Structure/Frontend.hs we find a Haskell encoding of this form:
-- | @Defun@ is the base defun structure
-- currently it does not have matching
data Defun = Defun
{ defunName :: Sexp.T,
defunArgs :: Sexp.T,
defunBody :: Sexp.T
}
deriving (Show)Note: Notice how we say nothing about the head being the cadr of the structure, and the arguments the caddr, and the body of course the caddr. Instead, we just lay out the logical structures in a record, divorced from any representation.
We provide an API to deal with the actual representation. It would need to change with a lisp-form redesign.
----------------------------------------
-- Defun
----------------------------------------
nameDefun :: NameSymbol.T
nameDefun = ":defun"
isDefun :: Sexp.T -> Bool
isDefun (Sexp.Cons form _) = Sexp.isAtomNamed form nameDefun
isDefun _ = False
toDefun :: Sexp.T -> Maybe Defun
toDefun form
| isDefun form =
case form of
_Defun Sexp.:> sexp1 Sexp.:> sexp2 Sexp.:> sexp3 Sexp.:> Sexp.Nil ->
Defun sexp1 sexp2 sexp3 |> Just
_ ->
Nothing
| otherwise =
Nothing
fromDefun :: Defun -> Sexp.T
fromDefun (Defun sexp1 sexp2 sexp3) =
Sexp.list [Sexp.atom nameDefun, sexp1, sexp2, sexp3]All records in that file have a corresponding interface
of name<structure>, is<structure>, to<strcuture>, and
from<structure>. These deal with the small details of cars and
cdrs.
This can be tested by opening the Easy file in the Juvix repl and running
λ> Right defun = Sexp.parse "(:defun foo (x) (:cond ((:infix == x 2) (:infix + 3 (:infix + 4 x))) (else (:infix + x 2))))"
λ> import qualified Juvix.Sexp.Structure as Structure
λ> Structure.toDefun defun
Just (Defun {defunName = "foo", defunArgs = ("x"), defunBody = (":cond" ((":infix" "==" "x" 2) (":infix" "+" 3 (":infix" "+" 4 "x"))) ("else" (":infix" "+" "x" 2)))})We can see this transformation agrees with our documentation.
What this buys us, is that when it comes time to do the passes, we don't have to worry about these details, while trying to make sure we don't change the semantics of the passes themselves. This properly decouples our concerns so we can worry about the abstraction meaning of the syntax in the passes while worrying about the details here.
However all is not fine, notice, we had to write nineteen lines of boilerplate in order to get rid of the details of the syntax! This is rather tedious, and if we count the numbers of these there are at least 22 structures in that file, and over 500 lines of this rather straightforward API. This is especially annoying given that we are essentially just translating over BNF translations.
It is due to this tedium early on that the lisp haskell generator was created. The code itself isn't the best (due to using string interpolation) and can with a bit of engineering be improved (with a proper S-expression DSL in the lisp code), however it works fairly well for our purposes.
Here are some choice snippets that cover every case of the generator
;; 1
(generate-haskell "Defun" '("sexp" "sexp" "sexp") ":defun")
;; 2
(generate-haskell "ArgBody" '("sexp" "sexp") nil)
;; 3
(generate-haskell "DeconBody" (repeat 2 "sexp") nil)
(generate-haskell "Case" '("sexp" "deconBody") "case" :list-star t)
;; 4
(generate-haskell "NotPunned" '("sexp" "sexp") nil)
(generate-haskell "RecordNoPunned" '("notPunnedGroup") ":record-no-pun"
:list-star t
:un-grouped t)
;; 5
(generate-haskell "ArgBody" '("sexp" "sexp") nil)
;; bodys here, as there are multiple!
(generate-haskell "LetMatch" '("sexp" "argBodys" "sexp") ":let-match")The first one correlates to the structure we've already seen. Namely the
Defunstruct. the first argument is the type name we wish to generate. This is of courseDefun. the second argument is the list we wish to parse, in this case it says all three arguments are justSexp.T's. and binds them in order toname,args, andbodyin the struct itself. The third argument is the name of the structure itself if it has one. Our lets are translated to the :defun structure, and so we note that here.The second case correlates to a very similar structure, except for that it lacks a name. so the structure we care about is
(arg body)with no name attached. Thenilin the third argument reflects this change.the third case correlates to a scenario with two changes. The first being is that we can define types for another to rely on. Here we are saying that case has the type
DecondBody, we use lower case to reflect the proper variable name this associates with. Further the:list-start taspect of this tells us that the last argument, in this case ofDeconBody, is the rest of the s-expression and not just thecadr.data Case = Case { caseOn :: Sexp.T, caseImplications :: [DeconBody] } deriving (Show)The fourth is the last new concept of the bunch, namely we have
:un-grouped t, which states the form in which this parses are not grouped like((name₁ type₁) (name₂ type₂) … (nameₙ typeₙ)), but rather(name₁ type₁ name₂ type₂ … nameₙ typeₙ).This means that we have to tell it explicitly that it occurs over 2 positions with that
:un-groupedargument.The fifth case is an interesting one. The key insight is that we say
argBodysrather thanargBody. This is because our generator is limited. Thus we manually write-- these are ungrouned fromArgBodys, where we groupBy2 both ways fromArgBodys :: [ArgBody] -> Sexp.T fromArgBodys = Sexp.unGroupBy2 . toStarList fromArgBody -- these are ungrouned fromArgBodys, where we groupBy2 both ways toArgBodys :: Sexp.T -> Maybe [ArgBody] toArgBodys = fromStarList toArgBody . Sexp.groupBy2To be able to handle the scenario where the list-star like form happens in not the last argument, but rather in a list in some other position!
Improvements Upon the Generator
The generator can be improved a lot, as the previous section mentions it was hacked together using string interpolation which is not a good structural way to handle this sort of problem. The alternative would however take a week of hacking, so it is not a priority to undergo.
However there are two worthwhile hacks that we should undergo.
Change the
Maybeof theto<Name>to anEither.This change at the current moment does not matter! Namely because
Nothingshould never be triggered. This is due to the parser in frontend excludes this possibility. However when syntax redesign comes in, this will no longer be the case. It would be great if the generated code could instead generate anEitherwhere the left counts the number of arguments given and states precisely why it can't translate the given S-expression form into the type we want.list-star like behavior anywhere. Currently we bake it into the last form, but it would be nice if we could have a way to denote this for the middle slots, so we can avoid hacks, like the manual
argBodysexample given in the last section.
Desugaring Passes
Now that we understand the structural underpinnings of the pass, we can now talk about the transformation itself.
We can observe the passes here.
There are two ways to proceed, if you don't want to go through the entire creation process of a pass you can skip the next section and go directly to reviewing a pass
The most important detail to note is that if you have a clear view of the input and output of pass, a pass should be easy to write and review. If creating this is hard, then I suggest reading through the next section to see the full life cycle of this process.
Creating a Pass
Instead of just showing an example, let us show writing one. Let us
define the cond transformation. We can find the form here.
It seems the Cond form is filled with a bunch of ((:infix ≡≡ x 3) 1)
forms which we can abstractly view as (<pred> <ans>). So let us
define these forms as a type. We do this in the Structure folder. In
particular we want to put this in Frontend.hs since this shows up in
the frontend syntax.
-- | @PredAns@ is an abstraction over questions and answers
data PredAns = PredAns {predAnsPredicate :: Sexp.T, predAnsAnswer :: Sexp.T}
deriving (Show)
-- | @Cond@ here Cond form takes a list of predicate answers
newtype Cond = Cond {condEntailments :: [PredAns]} deriving (Show)To reflect the structure we include the raw forms in the generator file and take the output of these calls into the Structure file.
(generate-haskell "PredAns" (repeat 2 "sexp") nil)
(generate-haskell "Cond" '("predAns") ":cond" :list-star t)Now we can test that we successfully matched the BNF by using the REPL
λ> Right cond = Sexp.parse "(:cond ((:infix == x 2) (:infix + 3 (:infix + 4 x))) (else (:infix + x 2)))"
λ> Structure.toCond cond
Just
(Cond
{condEntailments =
[PredAns { predAnsPredicate = (":infix" "==" "x" 2)
, predAnsAnswer = (":infix" "+" 3 (":infix" "+" 4 "x"))}
,PredAns { predAnsPredicate = "else"
, predAnsAnswer = (":infix" "+" "x" 2)}]})Now we know the shape of the data we are working with!
To get closer to the core version of match, let us first desugar this to an if. Something like
(:Cond (pred-1 result-1) … (pred-n result-n)) should turn into
(if pred-1 result-1 (if pred-2 result-2 (… (if pred-n result-n))))
So like cond, we also also define the records and forms we wish to work on
-- | @If@ has an pred, then, and else.
data If = If
{ ifPredicate :: Sexp.T,
ifConclusion :: Sexp.T,
ifAlternative :: Sexp.T
}
deriving (Show)
-- | @IfNoElse@ has a pred and a then.
data IfNoElse = IfNoElse
{ ifNoElsePredicate :: Sexp.T,
ifNoElseConclusion :: Sexp.T
}
deriving (Show)
-- In the generator
(generate-haskell "If" (repeat 3 "sexp") "if")
(generate-haskell "IfNoElse" (repeat 2 "sexp") "if")Because our generator is limited we make two variants.
Now let us write the form, first let us observe that we can view this
operation from cond to if as folding if over the list of
PredAns, with the result being an if with no else condition.
condToIf condExpression
| Just cond <- Structure.toCond condExpression,
-- we need to setup the if with no else
Just last <- lastMay (cond ^. entailments) =
let acc =
-- let's create it, with the predicate and answer of the
-- PredAns tye
Structure.IfNoElse (last ^. predicate) (last ^. answer)
|> Structure.fromIfNoElse
-- Now let us employ the fold strategy we talked about
in foldr generation acc (initSafe (cond ^. entailments))
| otherwise = error "malformed cond"
where
-- this is the folded function, see how we just build up the if,
-- then push it back to an s-expression at the end?
generation predAns acc =
Structure.If (predAns ^. predicate) (predAns ^. answer) acc
|> Structure.fromIfWith our current understanding we'd write something like this, and in fact we can test it as is! Just go to the Easy Pipeline file and include these dependencies and the function above.
import qualified Juvix.Sexp.Structure as Structure
import Juvix.Sexp.Structure.Lens
import Control.Lens hiding ((|>))Along with the definition and now we can see
λ> Right cond = Sexp.parse "(:cond ((:infix == x 2) (:infix + 3 (:infix + 4 x))) (else (:infix + x 2)))"
λ> condToIf cond
("if" (":infix" "==" "x" 2) (":infix" "+" 3 (":infix" "+" 4 "x")) ("if" "else" (":infix" "+" "x" 2)))We just created the bulk of our first pass! There is a few more details that one has to care about in a real pass, but we'll cover those in the reviewing section coming up
Reviewing a Pass
The following code can be found here.
-- | @condTransform@ - CondTransform turns the cond form of the fronted
-- language into a series of ifs
-- - BNF input form:
-- + (:Cond (pred-1 result-1) … (pred-n result-n))
-- - BNF output form:
-- + (if pred-1 result-1 (if pred-2 result-2 (… (if pred-n result-n))))
condTransform :: Sexp.T -> Sexp.T
condTransform xs = Sexp.foldPred xs (== Structure.nameCond) condToIf
where
condToIf atom cdr
| Just cond <- Structure.toCond (Sexp.Atom atom Sexp.:> cdr),
Just last <- lastMay (cond ^. entailments) =
let acc =
Structure.IfNoElse (last ^. predicate) (last ^. answer)
|> Structure.fromIfNoElse
in foldr generation acc (initSafe (cond ^. entailments))
|> Sexp.addMetaToCar atom
| otherwise = error "malformed cond"
--
generation predAns acc =
Structure.If (predAns ^. predicate) (predAns ^. answer) acc
|> Structure.fromIfWe saw most of this form in the creation of a pass section
above. However we will go over the rough strategy briefly. In order to
turn the input of cond to an if, we can view it as a fold, where
we fold the if form over the predicate and answers of the cond
structure with the accumulator being the already built up if's. We can
see this by the BNF comment at the start of the function. This
transformation gets us closer to the more primitive match
representation that is present in core.
We can see the implementation of this strategy shine through in the
body of condToIf and the folded function generation.
The main difference from our creation of a pass section is that we
have this Sexp.foldPred call, and that condToIf has two
arguments. The impotence of this is that Sexp.foldPred searches the
entire S-expression structure for the name Structure.nameCond, which
is :cond. When it sees this function it breaks the structure into
the atom, :cond, and the cdr which is the rest of the
structure. This means that if you run this on any form that contains
the cond form, then it will automatically run this transformation
for you!
The last key bit of information is Sexp.addMetaToCar atom, this is
to preserve meta information like line-numbers that were on the
:cond atom that we would like on our newly generated if atom.
Overall, reviewing a pass is rather easy, just keep in mind what the input form is, and what the output form is. As long as the output form is getting closer to the Core representation of matters, we have a successful pass.
To verify this pass, we can easily run it for ourselves and see if the
BNF Comment is being truthful.
λ> Pass.condTransform cond
λ> Right cond = Sexp.parse "(:defun f (x) (:cond ((:infix == x 2) (:infix + 3 (:infix + 4 x))) (else (:infix + x 2))))"
λ> cond
(":defun" "f" ("x")
(":cond" ((":infix" "==" "x" 2) (":infix" "+" 3 (":infix" "+" 4 "x")))
("else" (":infix" "+" "x" 2))))
λ> Pass.condTransform cond
(":defun" "f" ("x")
("if" (":infix" "==" "x" 2)
(":infix" "+" 3 (":infix" "+" 4 "x"))
("if" "else"
(":infix" "+" "x" 2))))Although we used the cond pass to talk about how these passes work,
we only do so to have a simple example of how these work. All the
other passes follow the same format and can be dissected by the same
thought process.
Context
The context phase is an important phase, this is where we start to introduce the context and our operations start to revolve around it. This is also where our pipeline starts to show some inadequacies with how we ingest data. But first we must talk about how we transform our list of S-expressions into a context
Contextify
We call this phase Contextify, or Contextualization. The files we
will first be investigating is split among many files, so we will link
them before we write code rather than at the start.