This the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

Pipeline

Documentation on the Juvix compiler pipeline

1: Idealized Pipeline

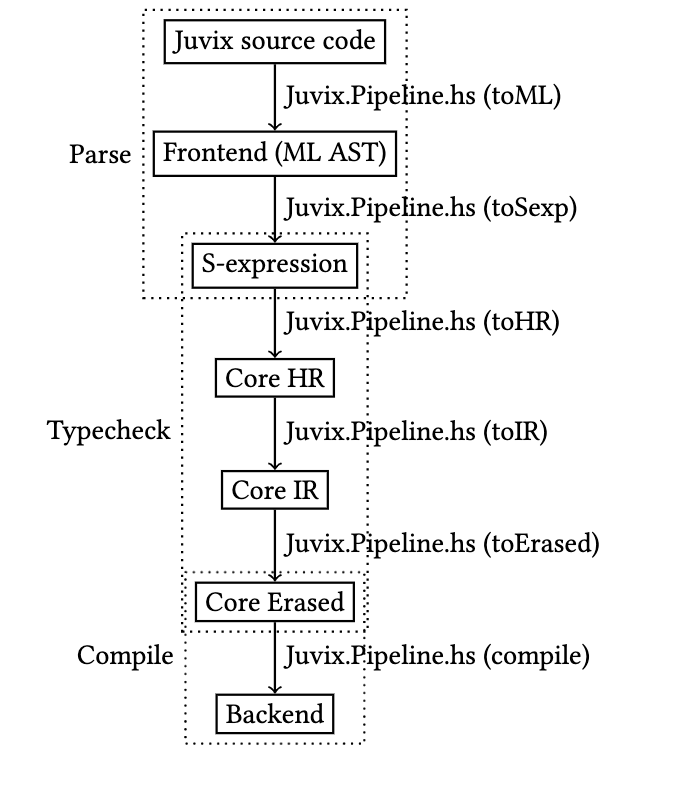
Pipeline

This section provides an overview of the compiler pipeline, from a source text file to the specific backend calls to produce the binary.

The in code explanation in that image can be itself be more boxed into what we see in app/main.hs

  Compile fin fout (Michelson backend) ->
    liftIO (readFile fin)
      >>= Pipeline.parse
      >>= Pipeline.typecheck @Pipeline.BMichelson
      >>= Pipeline.compile @Pipeline.BMichelson
      >>= Pipeline.writeout fout
      >>= liftIO . print

Parsing

The first set of phases to happen is that the text file is turned into a structured document, namely an ML AST.

Transition

This is a long phase of the compiler where we do a few things.

The first is that we desugar the expression using baked in expansions. This happens for function definitions, punned arguments, etc.
After that, we then take the desugared s-expressions and put them in our global "context". We do some extra processing in this stage as well like resolving what modules open each other.
- A context is like a primitive image. It can access all the information in a nested hashtable of sorts.
We still have a few more passes to run, as phases like symbol resolution and infix resolution can be run now.
Finally we have one last pass, translating what is left of the S-expression AST into a format where Core understands.

Core

Currently in our compiler the Pipeline.typecheck and Pipeline.compile function are backend specific, however the general transformations are similar regardless of the backend.

HR

This layer of core stand for Human Readable, as we have variable names instead of hairy de-bruijn indices. This phase is shortly lived, as most processing at this level wants to work on some extension of the Internal Representation as names create issues for the various algorithms.

IR

This is where the main process of type checking happens.

Names are reduced to de-bruijn indices.
We have many extensions with metadata that fluctuate depending on what pass of core is run.

Eliminations

In this phase of Core, we remove the types from the terms, as they don't serve any computation purpose. By this point we've done most of the processing we need.

In the future I suspect inlining algorithms will either be done here or in IR right above.

Backends

Michelson

LLVM

Arithmetic Circuit

1 - Idealized Pipeline

An Idealized version of our Core pipeline

This page covers what an idealized version of our core pipeline should look like for the time being.

The sections are laid out as followings.

The Pipeline defines the overall structure of the pipeline with comments between each step
Pipeline Function as a BNF with Examples gives a more long form BNF along with examples and commentary about the function. Further at the bottom of each section is a link to the reference for any literature that may be or may not be relevant.
The Outstanding section asks open questions about our passes and what questions arise that we don't have good answers to yet.
The Exhibition section gives further examples of a few key points when noted elsewhere in this document
The References section is where further links go about any related subjects

Pipeline

  patternMatchPipeline :: [(Pats,RHS)] ⟶ Type ⟶ ???
  patternMatchPipeline patternClauses type' =
    terminationChecking patternClauses type'
    |> corePipline

  -- The @corePipeline@ works over a context and an expression. The
  -- context is preserved throughout the computation as it's needed for
  -- many of these steps
  corePipeline ∷ Context ⟶ Expression ⟶ ???
  corePipeline form =
    -- Need to lambda lift pattern matching let abstractions, we don't
    -- worry about them here, instead we have the corePipeline go over
    -- those
    lambdaLiftLocalMatches form
    -- Local lets are simply just have guards left, we can remove both
    -- the top level guards here, and the let local guards.
    -- Once we realize this, we can also notice that lets can only be
    -- a single form.

    -- TODO ∷ we currently don't have guards going down to this level, we
    --        discharge it as one of our first desugar passes
    |> removeGuardsAndSimplifyLetToSingleCase
    -- Here we turn lets which have arguments into letting a name over
    -- multiple lambdas
    |> localLetsIntoLambdas
    -- Move OUT ∷ Desugar pass/Macro pass once we have that
    |> openExpressionIntoLetOverOpenName
    -- Has to resolve inner modules, so we have to treat namesymbols as a
    -- term for forms in the closure
    -- see exhibition ⒈
    |> hrToIR
    -- This step should be moved to the effect block of typeCheckEvalLoop
    -- when we support first class opens
    |> nameResolution
    -- Here we have to reun infixResolution after nameResolution
    |> infixResolution
    -- toANF runs an algorithm that takes the current form, and creates a valid HTML
    -- ANF algo should run before ‘interactiveMode‘, so we can run algebraic effects
    |> toANF
    |> branch [pipelineTypedMacro, pipelineUntypedMacro]
    -- either go to interactiveMode or proceed to compilation
    -- eraseZeroUsages looks a the current form, and removes any
    -- values/terms that have zero usages attached to them
    |> eraseZeroUsages
    -- TODO ∷
    -- See Reference Inlining
    -- for some good analysis on when to inline
    -- Currently We inline all globals, which excludes pattern matching functions
    |> inlineAlgorithm
    -- For the backends we need names rather than de bruijn indices to
    -- compile. This step gives us back names
    |> restoreNameFromDeBruijn
    -- TODO ∷
    -- See Reference Fast Curry
    -- Here we want the eval-apply algorithm from the reference
    -- This will change the code to a form that can explicitly talk about currying.
    |> fastCurry
    -- We currently have this form. This computes the capture environment
    |> captureLambdaEnvironment
    -- In Michelson we want to branch off before this
    -- This pass we want to explicitly break a lambda into an
    -- environment-closure and the binder itself
    |> lambdaIntoExplicitBinderAndClosure


  pipelineUntypedMacro form =
    mutual [macroExpand, eval] form
    -- This is a mutually recursive step, due to how haskell works, we
    -- have to put it as 1 step, however if we could, we should be able
    -- to break it up and put labels to show it's explicitly recursive.
    |> mutal [typeCheckEvalLoop, interactiveMode]

  -- Requires research on
  pipelineTypedMacro form =
    -- If macros are typed, then it's recursive with typeCheck
    -- meta programming consturctions inside the context, so witch can use it
    mutual [typeCheck, macroExpand, eval, interactiveMode] form

  -- Interactive mode is a poor man’s REPL
  -- Initially, it displays the results from typechecking and then it
  -- restarts the whole process again
  interactiveMode form =
    -- return the result of the evaluation, and a derivation tree
    -- optionally read some code and return
    showResultAndDerTree form
    input <- readCode
    juvixPipeline input

Pipeline Function as a BNF with examples

Lambda Lift the Local Matches

BNF

  input-expresson ::=
      let <let-path-input>+ in <expression>
    | ...

  output-expression ::=
      let <let-name-output>+ in <expression>
    | ...

  let-pat-input   ::= <name> <pattern>* <guard>+
  let-name-output ::= <name> <name>* <guard>+

  guard? ::= \| <expression> = <expression>
           | <expression>

Examples

  (** Example 1 *)

  (* Input *)
  def example =
    let
      foo (Just x) = 5
      foo Nothing  = 6
    in foo (Just ())

  (* Output *)


  (* generated by the pass *)
  def #g:unique-name (Just x) = 5
      #g:unique-name Nothing  = 6

  def example =
    #g:unique-name (Just ())


  (** Example 2 *)

  (* Input *)
  def example =
    let foo x = 5 + x in
    foo 3

  (* Output *)
  def example =
    let foo x = 5 + x in
    foo 3

  (** Example 3 *)

  (* Input *)
  def example =
    let foo {x, y} = y + x in
    foo {x = 3, x = 5}



  (* Output *)
  (* generated by the pass *)
  def #g:unique-name {x, y} = x + y

  def example =
    let foo x = 5 + x in
    #g:unique-name {x = 3, x = 5}

Description
The Transformation takes any let expression with <patterns>*'s that are any form of pattern matching, into top level declarations that are uniquely named for use where the previous let expression was used.
If the let form has only simple patterns, then we leave it un-transformed, this can be seen in Example 2 in the above code.

Possible Complications

We have to lambda lift extra items which may not be related to this transform see this example

  (* Input *)
  def example =
    let
      def bar x = x
      def foo (Just x) = bar 5
          foo Nothing  = bar 6
    foo (bar (Just ()))


  (* Output *)

  def #g:unique-bar x = x

  def #g:unique-foo (Just x) = #g:unique-bar 5
      #g:unique-foo Nothing  = #g:unique-bar 6

  def example = #g:unique-foo (#g:unique-bar (Just ()))

Literature
See Lambda Lifting

Remove Guards, and Multiple lets to single let

NOTE, Multiple lets of the same function, not nested

BNF

  ;; Input
  input-expression ::=
      let <let-name-output>+ in <expression>
    | ...

  input-declaration ::=
      def <def-pattern-input>+
    | ...

  ;; Ouptut
  ouptut-expression ::=
      let <name> <name>* = <expression> in <expression>
    | ...

  ouptut-declaration ::=
      def <def-pattern-ouptut>+
    | ...

  ;; Helpers
  def-pattern-input ::= <name> <pattern>* <guard?>

  def-pattern-ouptut ::= <name> <pattern>* <expression>

  let-name-input ::= <name> <name>* <guard?>

  guard? ::= \| <expression> = <expression>
           | <expression>

Examples

  (** Example 1 *)

  (* Input *)
  def add-3 x =
    let bar y = 3 + y in
    bar x

  (* Output *)
  def add-3 x =
    let bar y = 3 + y in
    bar x

  (** Example 2 *)

  (* Input *)
  def add-3-not-on-0 x =
    let compute y
         | y == 0 = Nothing
         | else   = Just (y + 3)
    in compute x

  (* Output *)
  def add-3-not-on-0 x =
    let compute y = if (Just (y + 3)) Nothing (y == 0)
    in compute x

  (** Example 3 *)

  (* Input *)
  def add-3-not-on-0 x =
    let compute y
         | y == 0 = Nothing
        compute y = Just (y + 3)
    in compute x

  (* Output *)
  def add-3-not-on-0 x =
    let compute y = if (Just (y + 3)) Nothing (y == 0)
    in compute x


  (** Example 4 *)

  (* Input *)
  def add-3-unless-1-or-0 x
    | x == 0 = 0
    | x == 1 = 1
    | else   = x + 3

  (* Output *)
  def add3-unless-1-or-0 x =
    if 0
       (if 1
           (x + 3)
           (x == 1))
       (x == 0)

  (* If is defined as follows *)
  (* about usages, consult the following table about
     what we can do usage wise
     cond
       first-class-usages? = if' (* comedy *)
       weakening?          = 1
       else                = ω *)
  sig if : {P : ((x : Bool) -0-> *))}
        -0-> t : P True
        -ω-> f : P False
        -ω-> b : Bool
        -1-> P b
  let if {Proof} then-case else-case True  = then-case
      if {Proof} then-case else-case False = else-case

Description
Here we do the majority of the work of removing guards from lets. We can notice that lets and defs can both at this point desugar their guard checks into dispatching to this if destructor function given.
We can also notice that after we run this, there can be no more lets with multiple patterns as both guards and matches have been handled now.

Possible Complications

We already handle guards in the desugar passes. Currently it just sees the guards as Cond's and desugars them into cases. This is however incorrect as pattern matching has a fall through behavior this does not respect.
- This can be solved with a proper pattern matching algorithm
This algorithm may be better served by the linearization algorithm given by the pattern match simplification. I'm not sure this is always possible in the def case. For the simple lets we currently have this works as a strategy however.

This could maybe also be served better with an with pattern through some strategy. See the following.


  (* Input *)
  sig foo : maybe (maybe int) -1-> int
  def foo (Just (Just x)) | x == 0      = 3
      foo (Just x)        | x == Just 3 = 5
      foo _                             = 0

  (* output *)
  sig foo-inner : maybe (maybe int) -1-> bool -1-> bool -1-> int
  def foo-inner (Just (Just x)) true _    = 3
      foo-inner (Just x)        _    true = 5
      foo-inner _               _    _    = 0

  sig foo : maybe (maybe int) -1-> int
  def foo m@(Just (Just x)) = foo-inner m (x == 0) false
      foo m@(Just x)        = foo-inner m false    (x == Just 3)
      foo m                 = foo-inner m false    false

Local Lets Into Lambdas

BNF

  input-expression ::=
      let <name> <name>* = <expression> in <expression>
    | ...

  output-expression ::=
      let <name> = <expression> in <expression>
    | ...

Examples

  (** Example 1 *)

  (* Input *)
  def foo =
    let bar a b c = a + b + c in
    bar 1 2 3

  (* Output *)
  def foo =
    let bar = λ a ⟶ (λ b ⟶ (λ c ⟶ a + b + c)) in
    bar 1 2 3

Description
Here we just take the given let form and transform it into it's pure lambda form for the body.
Possible Complications
- The type may need to be explicitly given, thus forcing us to give a signature with our bar.

Open Expression into Let Over Simple Open

BNF

  input-expression ::= open <expression> in <expression>
                     | ...

  output-expression ::= open <name> in <expression>
                      | ...

Examples

  (** Example 1 *)

  (* Input *)
  def foo =
    open bar in
    x + y

  (* Output *)
  def foo =
    open bar in
    x + y

  (** Example 2 *)

  (* Input *)
  def foo xs =
    open (fold building-up-a-module xs : mod {…}) in
    x + y

  (* Output *)
  def foo xs =
    let sig #:gensym 1 : mod {…}
        def #:gensym = fold building-up-a-module xs
    open #:gensym in
    x + y

Description
Here we want to have any non trivial open converted into a form where we let a name bind to this complicated expression and then have that name be used once in the open expression.
Possible Complications
- There is an outstanding question of how opens relate to de-buijn indicies.
  - Maybe name resolution can help sort this out?
- Type resolution of the module is also an interesting question to answer as well.
Literature

HR to IR

BNF

  term-input ::= λ <name> ⟶ <expression>
               | let <usage> <name> ...
               | sig <usage> <name> ...
               | pi  <usage> <name> ...
               | ...

  term-output = λ ⟶ <expression>
               | let <usage> = <expression>
               | sig <usage> ...
               | pi  <usage> ...

Examples

  (** Example 1 *)

  (* Input *)
  def foo a b =
    let add-them = a + b in
    λ d ⟶ d + add-them

  (* Output *)
  def foo (Global-Pat 0) (Global-pat 1) =
    let (global-pat 0 + global-pat 1) in
    λ ⟶ indicy 0 + indicy 1

  (** Example 2 *)

  (* Input *)
  def foo (Just a) (List b c d) =
    let add-them = a + b in
    λ d : (Π 0 (x : Nat.t) Nat.t)  ⟶ d + add-them + c + d

  (* Output *)
  def foo (Just (Global-pat 0))
          (List (Global-pat 1) (Global-pat 2) (Global-pat 3)) =
    let (global-pat 0 + global-pat 1) in
    λ : (Π 1 Nat.t Nat.t)  ⟶ indicy 0 + indicy 1 + global-pat 2 + global-pat 3

  (** Example 3 *)

  (* Input *)
  def foo (Just a) (List b c d) =
    let add-them = a + b in
    λ typ : (Π 0 (typ : ×₀) (Π 1 typ typ))  ⟶
      λ d ⟶
        d + add-them + c + d

  (* Output *)
  def foo (Just (Global-pat 0))
          (List (Global-pat 1) (Global-pat 2) (Global-pat 3)) =
    let (global-pat 0 + global-pat 1) in
    λ : (Π 0 ×₀ (Π 1 (indicy 0) (indicy 1))) ⟶
     λ ⟶
       indicy 0 + indicy 2 + global-pat 2 + global-pat 3

Literature
See De Bruijn
Description
Here we simply run a simple De Bruijn algorithm. In our code base this is actually already fully implemented
Possible Complications
- Bug see issue #864, namely we are inconsistent about how we handle recursive lets
  - Local recursive functions have to be lambda lifted per discussion
- How do we treat opens in terms of de-bruijn indicies?

Name Resolution

BNF

  input-expression ::= open <name> in <input-expression>
                     | ...
  ;; remove open
  ;; Note that in more complex cases this may not be possible, so we may
  ;; not have any bnf changes in this pass
  output-expression ::= ...

Examples

  (** Example 1 *)

  (* Input 1 *)

  (* Written by the user, which is part of the env by now *)
  open Prelude

  (* Input we see at this level *)
  sig add-list : Int.t -> List.t Int.t -> Int.t
  def
    add-list (global-pat 0) (Cons (global-pat 1) (global-pat 2)) =
      open Michelson in
      (* + is in Michelson *)
      let global-pat 0 + global-pat 1 in
      add-list (indicy 0) (global-pat 2)
    add-list (global-pat 0) Nil =
      global-pat 0

  (* Output *)
  sig add-list :
    Prelude.Int.t Prelude.-> Prelude.List.t Prelude.Int.t Prelude.-> Prelude.Int.t
  def
    add-list (global-pat 0) (Prelude.Cons (global-pat 1) (global-pat 2)) =
      open Prelude.Michelson in
      (* + is in Michelson *)
      let global-pat 0 Prelude.Michelson.+ global-pat 1 in
      add-list (indicy 0) (global-pat 2)
    add-list (global-pat 0) Prelude.Nil =
      global-pat 0

Description
Here we run name resolution, for top level opens, this is rather simple, as our current Contextify step notes top level opens. Thus what needs to be respected is how opens effect the closure and determine for that what is referencing to outer names.
Possible Complications
- To get complex opens working, we need to do some form of type checking. Thus this might have to be integrated to some level of type checking.
Literature

Infix Resolution

BNF

  input-expression ::= <input-expression> <op> <input-expression>
                     | ...

  output-expression ::= ...

Examples

  (** Example 1 *)

  (* Input *)
  (* * has precedence left 6  *)
  (* + has precedence 5  *)
  def foo = a * b * d + c

  (* Output *)
  def foo = + (* a (* b d))
              c

Description
Here we have to resolve infix symbols into prefix symbols given some precedence table. The easiest way to do this is to modify the Shunt Yard algorithm slightly for the constraints of Juvix. Thankfully this is already in.
Possible Complications
- One has to be careful about how infixl, infixr and infix all interact with each other.
Literature
See Shunt Yard

To ANF

BNF
Examples
Description
Possible Complications
Literature

Mutual Block

Type Checker

BNF
Examples
Description
Possible Complications
Literature

Witch

BNF
Examples
Description
Possible Complications
Literature

Erase Zero Usages

BNF
```
  ;; No BNF changes
```

Examples

  (** Example 1 *)
  (* Example may be artificial *)
  (* Input *)
  sig linear-comb-pos-nats
    : Π 1 Nat.t
         (Π 1 Nat.t
              (Π 2 Nat.t
                   (Π 0 (>= (indicy 0) 1)
                        (Π 0 (>= (indicy 2) 2)
                             (refinement Nat.t (> (indicy 0) 1))))))
  (* global-pat 3 and global-pat 4 are the 0 usage proofs *)
  def pos-linear-comb (global-pat 0)
                      (global-pat 1)
                      (global-pat 2)
                      (global-pat 3)
                      (global-pat 4) =
    let ( * (global-pat 2) (global-pat 1)) : 1 Nat.t in
    (* Let's prove that our result is at least (max (arg 1) (arg 2)),
       using our proofs of (arg 3) and (arg 4) *)
    let times-by-ℕ⁺-is-greater (indicy 0) (global-pat 3) (global-pat 4) : 0 Nat.t in
    refinement (+ (indicy 1) ( * (global-pat 0) (global-pat 3))) (indicy 0)
  (* Output *)

  sig linear-comb-pos-nats
    : Π 1 Nat.t
         (Π 1 Nat.t
              (Π 2 Nat.t
                   (Π 0 (>= (indicy 0) 1)
                        (Π 0 (>= (indicy 2) 2)
                             (Refinement Nat.t (> (indicy 0) 1))))))
  (* global-pat 3 and global-pat 4 are the 0 usage proofs *)
  def pos-linear-comb (global-pat 0)
                      (global-pat 1)
                      (global-pat 2)
                      (global-pat 3)
                      (global-pat 4) =
    let ( * (global-pat 2) (global-pat 1)) : 1 Nat.t in
    (+ (indicy 0) ( * (global-pat 0) (global-pat 2)))

Description
In this code we want to remove any code which has 0 usages in them. In particular, we can see in Example 1 that the proof about the number being greater than 1 is fully erased.
However, it is important to note a few points. We did not erase the passing of extra arguments to linear-comb-pos-nats. This is because these arguments are still passed on the application side, both in existing code and in any incremental compilation passes. These arguments are ignored. Alternatively, we could chose a strategy such that it's noted what the 0 usage arguments are, but have a shim layer that transforms arguments before application with functions with 0 argument functions.
Possible Complications
- What to do with 0 usage function arguments. See Description for another method of doing this.
- What do we do about top level records usage wise? We need the 0 usage arguments, so we have to treat them in an interesting way.
- We need to preserve signatures which only partially care about usage erasure.
Literature

Inline Algorithm

BNF
Examples
Description
Possible Complications
Literature

Restore name from De Bruijn indicies

BNF
Examples
Description
Possible Complications
Literature

Fast Curry

BNF
Examples
Description
Possible Complications
Literature

Capture Lambda Environment

BNF
Examples
Description
Possible Complications
Literature

Lambda Into Binder and Closure

BNF
Examples
Description
Possible Complications
Literature

Outstanding questions

How to Deal with Expansion?

Need eval? How does this reflect in the pipeline

Types of Macros?

How do we properly type it

Algebraic effects without Algebraic effects?

We want to structure the typeCheckEvalLoop as follows

  throw CantResolveSymbol ~> nameResolution

  -- typeChecking does
  -- Hole insertion, unifier, Type Checking, nameResolution
  typeCheckEvalLoop =
    doesAthing
      {resolverEffects
          = {
            -- filling holes
            , UnifyImplicits    ~> unifier
            -- Creating holes for the unifier to fill
            , InsertImplicit    ~> implicitInsertion
            -- For evaling terms
            , Evaluate          ~> eval
            -- For first class Name Resolution
            , CantResolveSymbol ~> nameResolution
            }}

Exhibition

⒈

def bar =
  let
    mod baz =
      mod biz =
        def foo = 3.
  baz.biz.foo
   ~> 0.biz.foo
   ~> resolve-symbol (resolve-symbol foo biz) 0

⒉ openExpressionIntoSimpleOpenPlusLet

def bar =
  let mod bar =
      def foo = 3.
  let #g:gensym = (bar djfka djfkas dfjak)
  open #g:gensym ~> open with type {foo}
  resolve-symbol foo #g:gensym.

def bar =
  let mod bar x y z =
        def foo = 3.
  let #g:gensym = (bar djfka djfkas dfjak)
  open #g:gensym ~> open with type {foo}
  resolve-symbol foo #g:gensym.


def bar =
  let mod bar x y z =
        def foo = 3.
  open (fold function-generating-a-module xs : mod {…})
  resolve-symbol foo #g:gensym.

def bar =
  let mod bar x y z =
        def foo = 3.
  let def #g:gensym =
        fold function-generating-a-module xs : mod {…}
  open-simple #g:gensym
  resolve-symbol foo #g:gensym.

References

De Bruijn Indicies

Benjamin C. Pierce: Types and Programming Languages chapter 6 page 75-80

Shunt Yard

Shunt Yard Algorithm

Template

BNF
Examples
Description
Possible Complications
Literature

Pipeline

Pipeline

Parsing

Transition

Core

HR

IR

Eliminations

Backends

Michelson

LLVM

Arithmetic Circuit

1 - Idealized Pipeline

Pipeline

Pipeline Function as a BNF with examples

Lambda Lift the Local Matches

Remove Guards, and Multiple lets to single let

Local Lets Into Lambdas

Open Expression into Let Over Simple Open

HR to IR

Name Resolution

Infix Resolution

To ANF

Mutual Block

Type Checker

Witch

Erase Zero Usages

Inline Algorithm

Restore name from De Bruijn indicies

Fast Curry

Capture Lambda Environment

Lambda Into Binder and Closure

Outstanding questions

How to Deal with Expansion?

Types of Macros?

Algebraic effects without Algebraic effects?

Exhibition

⒈

⒉ openExpressionIntoSimpleOpenPlusLet

References

Inlining

Fast Curry

Lambda Lifting

De Bruijn Indicies

Shunt Yard

Template