This the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

Core

Talks about various aspects of the Core code-base

1: HR
2: IR

2.1: Representation
2.2: Extensions
2.3: Evaluator

3: Original QTT Erasure algorithm
4: HR IR Conversion
5: Type Theory

5.1: Foundations
5.2: Inductive data types

6: Typechecker

6.1: Overview
6.2: Correspondences
6.3: Modules
6.4: Formalization

Type Theory

Our Core type theory, called "Quantitative Type Theory" ("QTT"), is derived from the paper I Got Plenty o’ Nuttin’. Modifications and extensions are documented here.

Extensions/Annotations

Core works off a system of annotations/extensions. These currently are crucial for understanding what happens to the data structures in Core.

More can be read about our extensible system here.

HR

HR is the first step into core from the frontend language. This phase is a lot like IR (Read below), however it includes names rather than De Brujin indices. Due to this, this phase is rather short lived.

Characteristics of HR

Is an Extension of HR with Names
Short Lived

IR

IR is the representation of Core in which all other extensions are based off of. In order to facilitate fast evaluation Core is broken up into terms and values. Values are like terms but they have no β-redexs via type construction. Thus they statically rule out λ being applied to arguments. This means values are in normal form.

Characteristics of IR

De Brujin indices
Extensions via Extensible
Idea of terms and values
- Values have no β-redexs by construction
  - Free name can still be there, and could be inlined
  - Impossible to reduce if the Free names are a data type function

Extension Layout and mapping

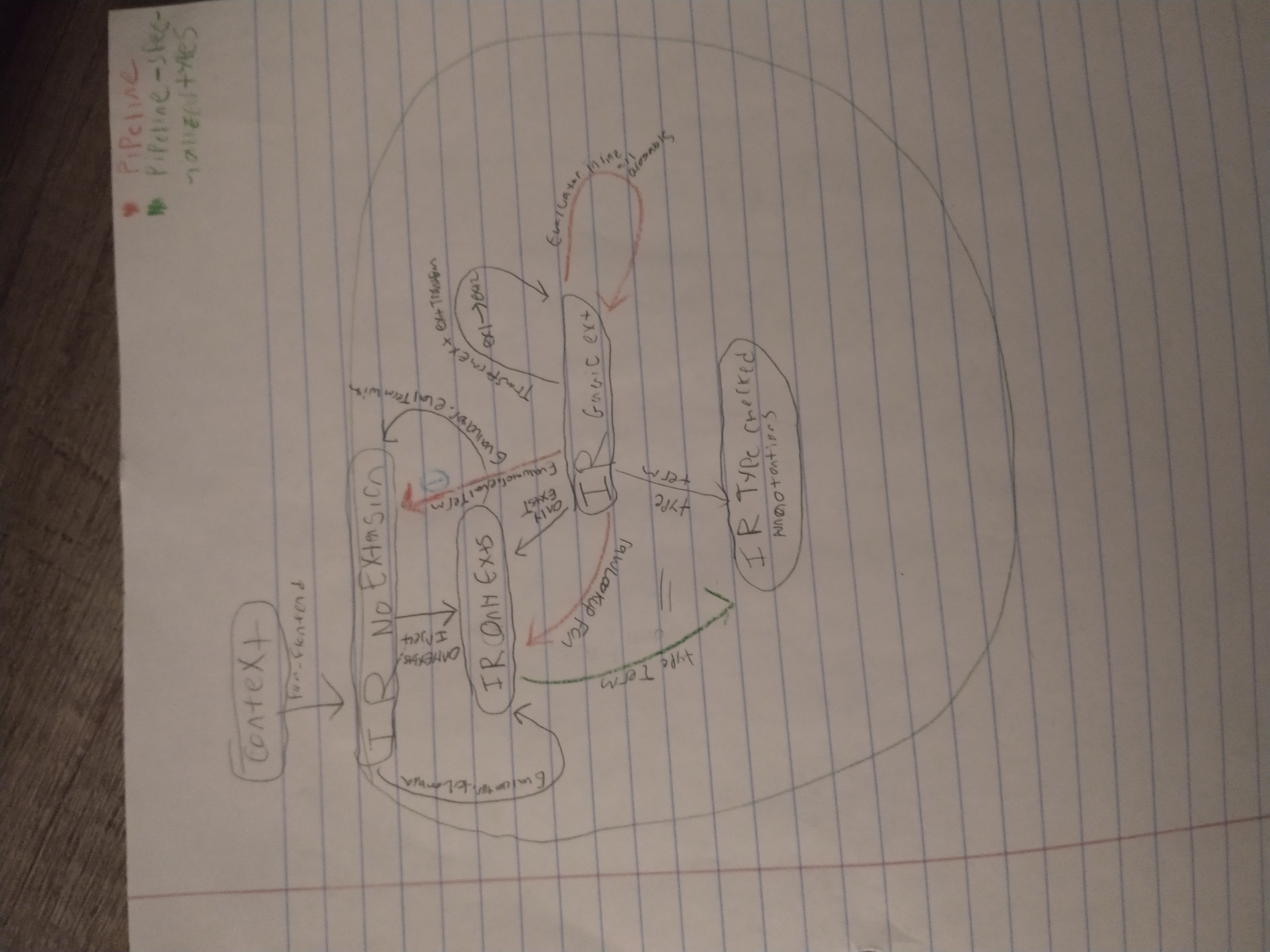
- In this diagram we can see various mappings that happen through the extensions of core.
Main representation

Type Checker

Type checking is the first phase of IR. This phase annotates every node with its type and usage. To facilitate fast type checking every type annotated is a fully evaluated value. Other phases like the unifier use this concept as well.

Erased

After the code gets pass through IR, we then want to erase all the type annotations we've built up. To do this, we send the code through the Erased representation. Unlike HR, Erased is not an extension of IR.

Erased also erases all forms which have 0 usages. Since usages are not first class yet, this is a rather simple.

Another key characteristic of Erased is that types are separate from Terms as they are currently assumed to have 0 usages. Thus types are always erased and separated out.

This may change with time.

ErasedAnn

This is the backend specific form that Michelson uses.

1 - HR

Replaces bound and free with just names, has names in the binders

Extension of IR
replace free and bound by var
Contains a map of namesybmols

Place for Pretty printing

Substitution

Translates into IR

State monad with traversal

2 - IR

2.1 - Representation

Representation

Global

A lot of the global information predates the frontend context. A lot can probably be integrated.
Raw Globals Type is a term, which may not be correct (what the user wrote), Regular global the types are values, which can be checked for equality eaiser.
- Only safe to eval something after it's been type checked
- Way to unify?

2.2 - Extensions

Extensions

Extensions are an important part of Core IR. They allow certain kinds of transformations

Transformation

2.3 - Evaluator

Evaluation of the internal representation in Juvix plays an important part in the compilation pipeline: it simplifies the program before passing it to the backend. As the internal representation is closely related to the λ-calculus with de Bruijn indices, the evaluator implements all necessary functions to do so.

In addition to the evaluation functions, the module provides functions for inlining globals (inlineAllGlobals / inlineAllGlobalsElim), turning function definitions into anonymous functions (toLambda), lookup functions for variables and filtering functions for extensions.

For more information on the λ-calculus with de Bruijn indices, see Wikipedia article. This document will describe the way the theory is implemented for Juvix, and expects a basic understanding of the λ-calculus with de Bruijn indices.

Substitution boils down to replacing the variables bound under the current λ, after which the free variables in the term need to be updated to reflect the removal of an abstraction layer, this is the task of weakening.

Substitution

Substitution lies at the core of evaluation, replacing bound variables with terms. Currently the compiler contains several closely related substitution implementations, both for terms and patterns. All of them serve the same purpose, but differ slightly in their types.

Term substitution

substWith: Substitutes any term a with an IR.Elim', but results in a term of type a.
substTermWith: Substitutes any term a with an IR.Elim', and results in an IR.Elim'.
gsubstWith: Generic substitution of f t with an IR.Elim', and results an f t again. This generic is used for automatic deriving of instances using GHC.Generics.

Pattern substitution

The functions are for substituting patterns, each of them take:

A number indicating the current traversal depth.
A IR.PatternMap containing pairs of pattern variables and terms.

All the functions return an Either with a PatternVar in case not substitution has happened, and the resulting term in case of a substitution.

patSubst': Substitutes any term a with any of the patterns provided in the map, and results in an a.
patSubstTerm': Substitutes any term a with any of the patterns provided in the map, and results in an IR.Term'.
gpatSubst': Generic substitution any term f t with any of the patterns provided in the map, and results in an f t. This generic is used for automatic deriving of instances using GHC.Generics.

Weakening

Weakening or shifting of de Bruijn indices is a central part of the evaluation. After performing β-reduction, any free variables need to be decreased to account for removal of the λ-abstraction.

The basic weakening function is weakBy', which takes:

An natural number, denoting the amount to shift free variables.
A cutoff value, for which all variables less than or equal are bound, and all variables greater than that are free. Typically this value will be 0, to denote that we want to account for removal of the outermost abstraction.
A term a to perform weakening / shifting on.

weakBy' will return a term a again, on which the weakening has been executed. The generic function gweakBy' is similar, but takes an f t as term and returns an f t. It is used for automatic deriving of instances using GHC.Generics.

3 - Original QTT Erasure algorithm

This article explains the QTT Erasure algorithm in a higher-level language for an easier digestion

Original QTT Erasure algorithm

Disclaimer This text only explains the QTT Erasure algorithm, you must already be familiar with how QTT works.

Initially, the algorithm assumes that:

any typechecked term $t : \rho > T$ elaborates to a program p¹;
$\rho \neq 0$, since you want to make sure that your program actually has something to execute before translating it into runnable code;
the translation is into the untyped $\lambda$-calculus.

The whole algorithm traverses the tree of terms elaborating programs – given that dependent types are the zero resource being erased. For a more complex language, we should probably not merge QTT erasure with an actual elaboration phase.

The only terms affected by erasure are binding-dependent terms, in McBride’s calculus, it’s $\lambda$ abstraction and application.

The algorithm goes as follows:

for $\lambda$-abs with a zeroed resource,
- you have a variable $0 > x : S$ ² bound to a body $\rho t : T$;
- it elaborates to a program p of type $T$. Meaning, that $x$ won’t be consumed in p – as it was evaluated already – and, then, $p$ can proceed.
for $\lambda$-app with a zeroed resource,
- you have a function $f$ that takes a variable $0 x : S$;
- while within your context, you have a zeroed value $s : S$;
- given $f[s : S/x]$, p elaborates to the body $t : T$ of $f$. Meaning that what’s left for $f$ is the returning function when $s$ is applied.
- for all remaining terms, elaborate it as is.

The main idea of the paper is to pre-bind zeroed resources, making it unavailable to the elaborated program p. The main trick of the paper is to pair zeroed resources from $\lambda$-abs with zeroed resources from $\lambda$-app. McBride’s paper provides a proof that a zeroed application will always meet a zeroed $\lambda$ abstraction.

Resources

I Got Plenty o Nuttin by Conor McBride

McBride’s paper actually splits the whole semantics into checking and synthesis, following bi-directional typechecking. Implementing the recipe bi-directionally would be ideal since it provides a literal algorithm, here we explain it by assuming both checking and synthesis mean just checking. ↩︎
The 0 prefix means that the term has 0 usage. ↩︎

4 - HR IR Conversion

This article goes over some of the idea of HR to IR conversion

HR ⟷ IR Conversion

The Pass which can be found here deals with the conversion between Core HR and Core IR.

HR ⟶ IR

This phase simply removes the names from the HR form and constructs a De-Brujin index from the names given in HR.

The algorithm for this for Terms and Elims is rather simple
1. When we see a binder (Pi, Lam, Sig, or Let), push the name to the stack for the form in which it is scoped over. Recurse and form and reconstruct said binder.
2. For forms without names, recurse and reconstruct.
3. When a name appears, look up it's index from the stack, this is the De-Brujin index we care about. If the Index is not there then we mark it as a Global

HR-Pattern's work in a different way, since patterns are disconnected from terms themselves and do not interact, they work on a system of registering pattern variables, when we come across the binder form =

Outstanding Questions

Since for Terms and Elims we don't account for pattern variables, and just mark everything unknown as Global, how does Pattern's affect this? It seems we would mark any PatternVar above this form as a Global and lose that information

IR ⟶ HR

This conversion adds back names to the IR form. This is mainly used for Pretty Printing.

The algorithm for Terms and Elims is once again rather simple
1. When we see a binder (Pi, Lam, Sig, or Let), generate a new name, and push it to the stack. Recurse and form the reconsturct said binder
2. Forms without names just recurse and reconsturct.
3. When a name appears, lookup the index from the stack, that position is the name which we care about.

5 - Type Theory

The type theory implemented by Juvix

5.1 - Foundations

Foundations of Juvix’s type theory

Quantitative Type Theory

Core's type theory, called "Quantitative Type Theory" ("QTT"), is derived from the paper I Got Plenty o’ Nuttin’. Further references for QTT include:

5.2 - Inductive data types

Juvix’s inductive data types

Juvix extends QTT with inductive data types.

6 - Typechecker

Core IR types and type-checking

6.1 - Overview

Overview of Typechecker’s place in Core

Where Typechecker fits into the pipeline

The typechecker is called via typeTerm, which in turn is called by typecheckErase and typecheckEval, ultimately via coreToAnn, which in turn is called by the backend-specific typecheck functions (which will soon be factored out into a common Pipeline.typecheck function), which fits between Pipeline.parse and Pipeline.compile.

I believe that once function typechecking is implemented, typecheckErase and typecheckEval will also need to call typeCheckDeclaration.

Overall structure

IR/Types/Base.hs defines the elements of the syntax of QTT: terms, values, variables, and patterns.

IR/Types/Globals.hs defines the main compound types derived from the Base types: functions and datatypes.

IRAnn/Types.hs defines the typechecker-specific annotations which correspond to the kinds of terms in QTT.

IR/CheckDatatype.hs and IR/CheckTerm.hs enforce the typing rules of QTT.

Interactions with other components

The typechecker imports back-end-specific types through Parameterisation.
Characteristically of a dependently-typed system, the Typechecker uses types and functions from the Evaluator, for example in:
- Typechecker's CanTC and Error types
- typeCheckConstructor, which has to evaluate the terms of the telescope passed to it
- typeTerm' and typeElim', which must perform reductions on terms to perform type-checking, in accordance with QTT's PRE and POST rules (characteristically of a dependently-typed theory)

Open questions / things I don't understand

6.2 - Correspondences

Correspondences between Typechecker code and QTT paper

Correspondences between `Typechecker` and QTT typing/evaluation rules

In this section we examine where the formal elements of Juvix's implementaion of Quantitative Type Theory appear in our implementation. $x=1$

Definitions 1 and 2 address generic rig s (ring without negation) as well as the 0, 1, many rig used by Idris-2. Neither of those has an explicit analogue in our code, since we use one specific rig, and not the one used by Idris-2 – rather, we use the natural numbers plus omega, which we call NatAndw.
Definition 3 defines sort ordering as a transitive relation on sorts which allows well-founded induction. This will be our subtyping relation, which is defined by the <: operator in IR/CheckTerm.hs.
Definition 4 is of term and elimination, which correspond to our Term and Elim defined in IR/Types/Base.hs.
Definition 5 is of contraction, reduction, and computation. Contraction is a single step of beta-reduction (substitution) or nu-reduction (stripping an annotation, which we can do once a term is fully computed), corresponding to "small-step" semantics. Computation is the reflexive-transitive closure thereof, corresponding to "big-step" semantics. We refer to computation as Evaluation, so the implementation of computation in our code is evalTerm (see the Evaluator documentation).
Definition 6 is of pre-context and context. The former is what is usually just called "context" in type theories – an association list of names to types. In QTT, the context is a mark-up of a pre-context with usages. In our typechecker, the pre-context is Context, and the mark-up is UContext.
Definition 7 is of prejudgment, which is what is usually just called "[type] judgment" in type theories; as QTT is presented bidirectionally, there is both a checking prejudgment (a Term is claimed to a given type) and a synthesis prejudgment (a given type is inferred for an Elim). Definition 8 is of a judgment as a prejudgment annotated with a usage. We don't explicitly use the term "judgment" in our QTT code, but the type judgments and usage judgments are captured by the Typechecker's specific extension to Annotation.
Definition 9 is of the type checking and synthesis rules. (This is extended later by definition 39, which includes erasure and computation. Those two are primarily subjects of other documents.) Below are some correspondences between the typing rules (from definition 9) and the implementations in our code. The explicit implementation of these rules is concentrated within typeTerm' and typeElim', and their helper functions, in CheckTerm.hs.
- PRE, POST: These rules, which state that a type may be used in place of another if the latter reduces to the former, are implemented in the IRAnn' case of typeElim', and as calls throughout the cases of typeTerm' to evalTC and substApp (which calls evalTC internally).
- SORT: The IR.Star' case of typeElim'. Stratification appears not to be fully implemented as of this writing – the call to requireUniverseLT is commented out.
- VAR: The IR.Bound' and (two – one for globals and one for patterns) IR.Free' cases of typeElim'.
- FUN: IR.Pi' case of typeTerm'
- LAM: IR.Lam' case of typeTerm'
- APP: IR.App' case of typeElim'
- ELIM: The requireSubtype call in the IR.Elim' case of typeTerm'.
- CUT: The call to typeElim' itself, in the IR.Elim' case of typeTerm'.
Definition 17, of subtyping, is implemented by the <: operator in IR/CheckTerm.hs.
Definitions 10-16 and 18-36, and all the Lemmas, all relate to reasoning about the typing system, rather than defining the type system, so they do not have direct analogues in our code (except maybe in some comments!). They could, however, if we were to implement Juvix in a dependently-typed language (or to at least some degree if we were to use Liquid Haskell) – such as Juvix itself.
Definitions 37 and on refer to Erasure and to computation (which we call Evaluation), each of which we document as a separate module, so we do not explore them here, except insofar as we have touched on some aspects where exploring definitions 9 and 39 together above.

6.3 - Modules

Documentation of individual Typechecker modules

Definitions by module (beneath `Core/`)

`Types`

Types used throughout the typechecker (at least I think that's the intent):

PipelineError
Includes TypecheckerError, which we currently exit with when a user program is incorrectly typed. (I expect the long-term plan is to produce from it a human-readable error message.)
PipelineLog
Used with @"log" (from Capability.Writer) to log a couple of types of events.
TermAssignment, AssignWithType
Maps from variables to formulae of Elementary Affine Logic (EAL) / Elementary Affine Core (EAL). These terms are translated to interaction nets, which Juvix uses as its execution model.
I didn't find any uses of these types that weren't ultimately within the InteractionNetIR module, so they should probably be moved there.

`IR`

Aliases for types and functions from IR/Typechecker.

`IR/`

Types
Aliases for types and functions from IR/Types/Base and IR/Types/Globals, and some simple queries on them. There is one significant pair of mutually recursive functions here: quote :: Value -> Term and neutralQuote :: Neutral -> Elim. (As we shall see below, a Neutral is a particular kind of Value, and may include a Value, hence the mutual recursion.)
Types/
- Base
  - The definitions in terms of primitive types of several internal types. For example, a BoundVar is represented by a Natural, and a PatternVar by an Int. Name s are either Global s or Pattern s; the implementation of GlobalName is defined in the NameSymbol library.
  - GlobalUsage is defined here and restricted to only Zero or Omega, but there is a TODO comment asking whether globals might have other usages.
  - Several of the most pervasive data types are defined here, all as extensible, in the sense of trees-that-grow, meaning that different modules can extend them in their own ways, to use their own specific types of annotations, producing versions with a ' suffix:
    - Term Since Juvix is dependently-typed, a type (PrimTy) is one kind of term.
    - Elim An Elim may be a bound variable, a free variable, an application of an Elim (to a Term), or a usage annotation. An Elim is also a term (it may be embedded in a Term with the Elim constructor). Elim is so-called because McBride calls this type an "elimination" in I Got Plenty o' Nuttin'.
      Elim may be viewed as a term that can be inferred (synthesized).
    - Value Since Juvix is dependently-typed, a type (VPrimTy) is one kind of value. Value's definition strongly resembles that of Term, but there are differences; for example, there are let Term s, but no let Value.
    - Neutral Neutral is to Value as Elim is to Term: A Neutral is a bound variable, a free variable, or an application of a Neutral (to a Value); a Neutral is also a Value (it may be embedded in a Value with the VNeutral constructor).
      A Neutral may be viewed as a "stuck term": one for which typechecking must be deferred until some other term(s) has/have been typechecked. (Perhaps this is the source of the name "neutral" – it's neither good (definitely typechecks) nor bad (definitely doesn't typecheck) yet?)
    - Pattern Patterns contain PVar s which are bound by successful pattern matches, as well as primitive values, terms, and pairs and lists of Pattern s.
- Globals
  - Many Constraint-valued definitions which allow multiple instance s of various classes for various types to be declared at once. (For example, RawGlobalAll allows any type which satisfies it to derive Show, Eq, and Data, among others.)
  - Several more pervasive types, built upon those in Base:
    - Pos, representing strict positivity (or otherwise)
    - FunClause', which defines the form of Juvix function definitions. It comprises arguments (a Telescope), a pattern match (a list of Pattern'), a body, a type, and Bool fields indicating whether the clause is a catchall and/or unreachable.
    - A Function' comprises a NonEmpty list of FunClause' s.
    - The widely-used DataArg' includes a name, a usage, and a type.
    - A Datatype' includes a name, DataArg' s (each with a Pos), a universe level, and a list of constructors (DataCon').
    - A type constructor – DataCon' – includes a name, a type, an the function which defines it (whose output type is the type of the constructor).
    - Raw forms of the above. In each case, the Raw form uses Term where the non-Raw (Cooked?) form uses Value.
Typechecker
There's only one definition in this module, but it's a big one: typeCheckDeclaration, which takes a telescope, a list of datatypes, and a list of functions, and calls typeCheckAllCons (see below) on each datatype in the list. If type-checking is successful, it adds the datatype and its constructors to the globals.
As I write, typeCheckDeclaration is incomplete: it doesn't use one of its parameters, the one comprising a list of function declarations; furthermore, nothing actually calls it yet (except itself, recursively). That is because we simply haven't gotten to writing the typechecking of functions yet (which is also why the backend-specific typecheck functions currently inline everything recursively starting with main).
Typechecker/
Some of the types in Typechecker/ are parameterized over back-ends through the Parameterisation type which each back-end exports.
- Types
  Contains typechecker-specific extensions of some core types:
  - Annotation': Adds usage and type.
  - BindAnnotation': Adds an Annotation' for both the binder and the term that introduces the binder (Lam or Let).
  - Term': Annotations for each of the constructors of Term s (pairs, pi-types, sigma-tyoes, Elim' s, and so on).
  - Elim': Annotations for each of the constructors of Elim s (bound and free variables and applications of them).
- Env
  The typechecker's extension of EnvCtx is a GlobalsT, which is a (hash)map of names to Global' s, which in turn may be datatypes, data constructors, functions, or Value s (with names and usages). Env therefore also defines a HasGlobals alias for HasReader "globals".
  The interaction with the evaluator, as required by dependent typing, appears in this module via the CanTC type, which requires instances for Eval.HasSubstValue, Eval.HasPatSubstTerm, and Eval.HasWeak.
  This module also defines a Context as a list of the typechecker-specific form of Annotation. There is also a usage context, UContext, which is a list of Usage.
  Pattern bindings and usages – PatBinds and PatUsages – are defined as IntMap s to annotations and usages, respectively, reflecting the use of de Bruijn indices.
  Env also defines the typechecker's State monad: InnerState, which contains a Parameterisation, a PatBinds map, and a Context. (There's a lot of boilerplate related to it.)
  Env also defines signatures: SigDef is a sum of function, constructor, and datatype signatures. Signature maps global names to SigDef s, so it represents all the signatures in global scope. Typechecking functions return Signature s through the TypeCheck type, which uses Capability, with the name "typeSigs".
- Error
  Defines which errors can occur during typechecking. TypeMismatch, for example, represents a unification error on a variable. Other errors largely follow the possible types of terms – universe mismatches, usage mismatches, non-function types where function types are expected, incompletely-applied data constructors, and unbound variables. Again because dependent typing makes the typechecker depend on the evaluator, the typechecker may also wrap an error from the evaluator (Core/IR/Evaluator/Types.Error).
  The module also provides pretty-printing and an exception wrapper for the main TypecheckError type.
CheckDatatype
Exports two interfaces, which between them allow the type-checking of datatype declarations; hence, both are called by typeCheckDeclaration :
- checkDataType
  Typechecks all the parameters of a datatype declaration, ultimately by calling typeTerm on each.
- typeCheckAllCons
  Typechecks all the constructors of a datatype declaration, ultimately by calling typeTerm on each, followed by evalTerm, because of the potential dependency of types on values.
CheckTerm
Exports typeTerm, through which the typechecker is plugged into the Pipeline, via typecheckEval and typecheckErase, and through them from coreToAnn, which is called from the backend-specific typecheck functions with the appropriate Parameterisation s. (The backend-specific typecheck functions in the current development branch, as I write, have a lot in common, but Alberto is factoring them out as part of PR 821.)
Internally, typeTerm is implemented in terms of the mutually-recursive typeTerm' and typeElim' (which follow the structures of the mutually-recursive Term and Elim). These two functions are, in a sense, the core of the typechecker: they're the expression in code of the typing rules of QTT. For example, when typeTerm' is given a lambda with expected type A -> B, it checks whether assuming that the variable has type A results in the body correctly typechecking (with a recursive call to typeTerm') with type B.
The mutual recursion expresses the bidirectionality of the type checking: annotated terms are checked by typeTerm' ; unannotated terms ("eliminations") have their types inferred (synthesized) by typeElim'.
(Note: as of this writing, there is a bug in the Pair' case of typeTerm' : it doesn't evaluate the left term in checking the type of the right, so it wouldn't handle dependent pairs correctly. I will fix that shortly.)
One of the types that appears as a frequent return value in CheckTerm.hs is Leftovers. This type keeps track of variables which haven't yet been used as often as their Usage annotation allows – and, if it's not omega, requires! Hence if there are any Leftovers with usages other than omega after a term has been type-checked, that causes a LeftoverUsage TypecheckerError to be thrown.
CheckTerm.hs is also the location of our definition of the subtyping relation, operator <:.
Many of the return values of functions in CheckTerm.hs are parameterised over Monad s with constraints such as HasThrowTC' and HasBound. So they expect to be able to throw TypecheckerError s, or to be called as part of the execution of a state monad containing (at least) a list of bindings. That's a pattern which strikes me as crying out for algebraic effects – I think they could make the signatures much more readable, with less boilerplate and less code to compose effects. So I feel this module should be able to "read" better when it's written in Juvix itself!
TransformExt
This module defines an interface for transforming one extension of a Term (in the sense of trees-that-grow) into another extension of Term – an applicative functor on term extensions. Such functors are defined in terms of their operations on each variant of Term, such as primitive, pi-type, let-binding, and so on. Such functors compose (and the TransformExt module define the compose function which composes them). This module also defines a forgetful functor, forgetter, which transforms an extended Term into a Term with no extension (NoExt).
There are forgetful uses in the Evaulator and Erasure modules, but I haven't found any non-forgetful uses yet.
TransformExt/
- OnlyExts
  OnlyExts is so-called because it defines a Term -transforming functor which discards annotations but preserves extensions.

`IRAnn/`

Types
The typechecker-specific annotation of terms comprises:
- A usage (any natural number, or omega)
- A term of QTT (which might be a type), which is one of:
  - * (a universe, of which there is a natural-number-indexed hierarchy)
  - a primitive type
  - a primitive constant
  - a pi-type (dependent product)
  - a lambda
  - a sigma type (dependent sum)
  - a pair
  - a let-binding
  - the unit type
  - the unit value
  - one of the Elim types:
    - a bound variable
    - a free variable
    - an application of an Elim to a Term
    - a Term annotated with a Usage
  Some of these terms are extensions to core QTT, which, for example, does not appear to me to define explicit pair types, for example.
Erasure
This module just defines two forgetful functors, for Term and Elim, which discard extensions (see TransformExt).

6.4 - Formalization

Formalization of QTT in Idris-2

Category-theoretic formalization of QTT: "Quantitative Categories with Families"

-- Following Definition 3.1, of "Categories with Families (CwFs)",
-- in _Syntax and Semantics of Quantitative Type Theory_.
record CwF where
  constructor MkCwF
  -- "C is a category..."
  Underlying : Category
  -- "...with a chosen terminal object T"
  Terminal : Object Underlying
  TerminalCorrect : Universality.IsTerminal {cat=Underlying} Terminal
  -- "For delta in Ob(C), a collection Ty(delta) of semantic types"
  SemanticType : Object Underlying -> Type
  -- "For delta in Ob(c) and S in Ty(delta), a collection Tm(delta, S) of
  -- semantic terms"
  SemanticTerm : (object : Object Underlying) -> SemanticType object -> Type
  -- "For every f : delta -> delta' in C, a function
  -- -{f} : Ty(delta') -> Ty(delta)..."
  MapType : (obj, obj' : Object Underlying) ->
            Morphism Underlying obj obj' ->
            SemanticType obj' -> SemanticType obj
  -- "...and for S in Ty(delta') a function
  -- -{f} : Tm(delta', S) -> Tm(delta, S{f})..."
  -- (Implementer's note:  I don't understand why both MapType and MapTerm
  -- (as I'm calling them) are referred to in the paper as "-{f}".  Is that
  -- a typo, or will they just distinguish between MapType and MapTerm by
  -- context?)
  MapTerm : (obj, obj' : Object Underlying) ->
            (f : Morphism Underlying obj obj') ->
            (S : SemanticType obj') ->
            SemanticTerm obj' S ->
            SemanticTerm obj (MapType obj obj' f S)
  -- "Such that both assignments preserve identity and composition"
  MapTypePreservesIdentity : (obj : Object Underlying) ->
                             (S : SemanticType obj) ->
                             MapType obj obj (Identity Underlying obj) S = S
  MapTypePreservesComposition : (a, b, c : Object Underlying) ->
                                (f : Morphism Underlying a b) ->
                                (g : Morphism Underlying b c) ->
                                MapType a c
                                  ((.*) {cat=Underlying} {a} {b} {c} g f) =
                                (MapType a b f) . (MapType b c g)
  MapTermPreservesIdentity : (obj : Object Underlying) ->
                             (S : SemanticType obj) ->
                             MapTerm obj obj (Identity Underlying obj) S = S
  MapTermPreservesComposition : (a, b, c : Object Underlying) ->
                                (f : Morphism Underlying a b) ->
                                (g : Morphism Underlying b c) ->
                                (S : SemanticType c) ->
                                (t : SemanticTerm c S) ->
                                MapTerm a c
                                  ((.*) {cat=Underlying} {a} {b} {c} g f) S t =
                                MapTerm a b f (MapType b c g S)
                                  (MapTerm b c g S t)
  -- "For each object delta in C and S in Ty(delta) an object delta.S (called
  --  the _comprehension of S_)..."
  Comprehension : (obj : Object Underlying) ->
    SemanticType obj -> Object Underlying
  -- "...such that there is a bijection natural in delta':"
  ComprehensionToMorphism :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    Morphism Underlying obj' (Comprehension obj S) ->
    Morphism Underlying obj' obj
  ComprehensionToTerm :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    (f : Morphism Underlying obj' (Comprehension obj S)) ->
    SemanticTerm obj'
      (MapType obj' obj (ComprehensionToMorphism obj S obj' f) S)
  TermToComprehension :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    (m : Morphism Underlying obj' obj) ->
    SemanticTerm obj' (MapType obj' obj m S) ->
    Morphism Underlying obj' (Comprehension obj S)
  ComprehensionToTermToComprehension_id :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    (f : Morphism Underlying obj' (Comprehension obj S)) ->
    TermToComprehension obj S obj'
      (ComprehensionToMorphism obj S obj' f)
      (ComprehensionToTerm obj S obj' f) =
    f
  TermToComprehensionToTerm_id_morphism :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    (m : Morphism Underlying obj' obj) ->
    (term : SemanticTerm obj' (MapType obj' obj m S)) ->
    ComprehensionToMorphism obj S obj' (TermToComprehension obj S obj' m term) =
    m
  TermToComprehensionToTerm_id_term :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj' : Object Underlying) ->
    (m : Morphism Underlying obj' obj) ->
    (term : SemanticTerm obj' (MapType obj' obj m S)) ->
    ComprehensionToTerm obj S obj' (TermToComprehension obj S obj' m term) =
    replace {p=(\m' => SemanticTerm obj' (MapType obj' obj m' S))}
      (sym (TermToComprehensionToTerm_id_morphism obj S obj' m term)) term
  ComprehensionToMorphismIsNatural :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj', obj'' : Object Underlying) ->
    (observerChange : ObserverChange {cat=Underlying} obj' obj'') ->
    -- I'm not sure whether it is necessary to impose naturality on the
    -- observer change in order to ensure it on the comprehension-to-morphism
    -- bijection; that's just a guess.  We could find out whether proofs would
    -- go through without it.
    (isNatural : ObserverChangeIsNatural
      {cat=Underlying} {observerA=obj'} {observerB=obj''} observerChange) ->
    (f : Morphism Underlying obj' (Comprehension obj S)) ->
    ComprehensionToMorphism obj S obj''
      (observerChange (Comprehension obj S) f) =
    observerChange obj (ComprehensionToMorphism obj S obj' f)
  ComprehensionToTermIsNatural :
    (obj : Object Underlying) -> (S : SemanticType obj) ->
    (obj', obj'' : Object Underlying) ->
    (observerChange : ObserverChange {cat=Underlying} obj' obj'') ->
    -- I'm not sure whether it is necessary to impose naturality on the
    -- observer change in order to ensure it on the comprehension-to-term
    -- bijection; that's just a guess.  We could find out whether proofs would
    -- go through without it.
    (isNatural : ObserverChangeIsNatural
      {cat=Underlying} {observerA=obj'} {observerB=obj''} observerChange) ->
    (f : Morphism Underlying obj' (Comprehension obj S)) ->
    ComprehensionToTerm obj S obj''
      (observerChange (Comprehension obj S) f) =
    MapTerm obj'' obj'
      (ObserverChangeInducedMorphism
        {cat=Underlying} {observerA=obj'} {observerB=obj''} observerChange)
      (MapType obj' obj (ComprehensionToMorphism obj S obj' f) S)
      (ComprehensionToTerm obj S obj' f)

Core

Type Theory

Extensions/Annotations

HR

Characteristics of HR

IR

Characteristics of IR

Extension Layout and mapping

Type Checker

Erased

ErasedAnn

1 - HR

Place for Pretty printing

Substitution

Translates into IR

2 - IR

2.1 - Representation

Representation

Global

2.2 - Extensions

Extensions

Transformation

2.3 - Evaluator

Substitution

Term substitution

Pattern substitution

Weakening

3 - Original QTT Erasure algorithm

Original QTT Erasure algorithm

Resources

4 - HR IR Conversion

HR ⟷ IR Conversion

HR ⟶ IR

Outstanding Questions

IR ⟶ HR

5 - Type Theory

5.1 - Foundations

Quantitative Type Theory

5.2 - Inductive data types

6 - Typechecker

6.1 - Overview

Where Typechecker fits into the pipeline

Overall structure

Interactions with other components

Open questions / things I don't understand

6.2 - Correspondences

Correspondences between Typechecker and QTT typing/evaluation rules

6.3 - Modules

Definitions by module (beneath Core/)

Types

IR

IR/

IRAnn/

6.4 - Formalization

Category-theoretic formalization of QTT: "Quantitative Categories with Families"

Correspondences between `Typechecker` and QTT typing/evaluation rules

Definitions by module (beneath `Core/`)

`Types`

`IR`

`IR/`

`IRAnn/`